
typical interference with two very close frequencies
(beat frequency = difference of the frequency between the two tones)
Piano tuners can detect differences in pitch of less than one Hertz and good piano tuners can match pitches within a hundred ppm or better. What do they hear? Two tones played together with nearly the same frequency will create an interference. On any point of listening these two tones will merge together into one tone increasing and diminishing in level with a so called beat frequency. This beat frequency represents exactly the difference in the frequency between the two tones. A merged tone going up and down in level every one second indicates a frequency difference of one Hertz between the two tones.
The higher the beat frequency is, the higher is the frequency difference between the two tones. From a certain point no beat is audible anymore and soon the first musical interval, the minor 2nd, can be heard between the two tones.

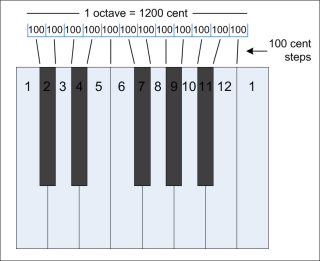
Musical intervals and differences in pitch are also evaluated in cent. One octave is divided into 1200 cent, each semi-tone in 100 cent (for the equal temperament, see below).
|
| one octave is divided in 1200 cent each semi-tone in 100 cent |
Using the 12-half-tone system, it is mathematically not possible to tune an instrument absolutely correctly.
A perfect fifth with the frequency ratio of 3:2 equals approximately 702 cents, on the basis that an octave has 1200 cent (see above). Dividing the octave into equal parts the fifth should equal 700 cent.
Only four scales could be played in conformity with the perfect 5th's and the minor and major 3rd's. A small remaining tonal difference must be partitioned. We talk of an amount of about 25 cent.
There have been several approaches over the last centuries of musical history to solve this problem. Especially Johann Sebastian Bach (the 'Well Tempered Clavier') was very active in this field. His motivation for composing the 'Well Tempered Clavier' was to demonstrate the varying key colors in the circle of fifths.
Several different methods were used over the centuries, creating different overall sounds of played music. Today normally the equal temperament is used. This system is based on the twelfth root of 2 and is called 12-TET (twelve-tone equal temperament).
12-TET
The twelve-tone equal temperament divides one octave into 12 equal parts. Twelve half-tones give a doubling of frequency and all of these half-tones are exactly the same. The main drawback to this equal temperament is that all major thirds are quite a bit off from where they ought to be, roughly 14% of a half-tone.
The ratio of frequencies for each half-tone is equal the twelfth root of two.
| Equal Temperament | |||
| Note | Frequency Ratio to Note 'C' ( 'Tone' (Hz) / 'C' (Hz) ) | Cent, individual step | Cent to 'C' |
| C | 1 | ||
| C# | 1.059463094 | 100 | 100 |
| D | 1.122462048 | 100 | 200 |
| Eb | 1.189207115 | 100 | 300 |
| E | 1.259921050 | 100 | 400 |
| F | 1.334839854 | 100 | 500 |
| F# | 1.414213562 | 100 | 600 |
| G | 1.498307077 | 100 | 700 |
| G# | 1.587401052 | 100 | 800 |
| A | 1.681792831 | 100 | 900 |
| A# | 1.781797436 | 100 | 1000 |
| B | 1.887748625 | 100 | 1100 |
| C | 2 | 100 | 1200 |